Too Many Knobs?

As I have written about models, I have talked about comparing models to observations of the processes that they are meant to represent. I talked briefly about model parameters and how they could be tuned to make an individual model better represent the data at hand. Each parameter is like a knob that can be turned to adjust the details of the given model.

For example let's consider the linear model illustrated below. In this model, factory output is assumed to be proportional to the input of labor. For a given increase in the hours worked, the factory produces a corresponding increase in output. The constant of proportionality (a, the slope of the line) and the amount of labor necessary to simply maintain the factory at zero output (the labor-axis intercept (b is actually the output-axis intercept)) may be different for different factories. A factory characterized by the red line will be more efficient and more productive than one characterized by the green line.



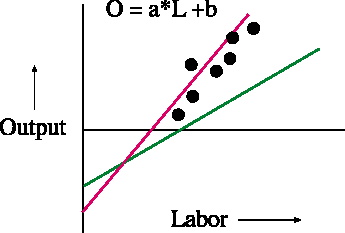
The dots in the figure are observations of the relationship between output and input from some factory. While the data are pretty linear, it is easy to imagine a line that would fit those data better than the ones I have drawn. The better fitting line would be described by adjusting the slope (a) downward and shifting the intercept to the right.

In the example above there are more data points than there are parameters and we may find that the best fitting line does not actually pass through any of the observations. The extent to which the data are close to the best fit model is a measure of how good the model fits the data; it can also be a measure of the certainty with which the model can be used to predict behavior in the future. The case where there are more data points than there are parameters is called over-determined; over-determined is good because it gives you a measure of certainty regarding the fit of the model to the data.

Now imagine we had only two data points. In that case there is exactly one line that fits the data exactly. This is ok, but we can fit those data equally well with any two-parameter model and we have no measure of certainty. It is generally true that you can exactly fit N data points with a model that has N parameters.

Good models have considerably fewer parameters than there are observations to constrain the model. As models become more complex they acquire more tunable parameters. In the case of GCMs there are many many tunable parameters, but there are also many many observations to constrain the models.

In using models to help us think about how Earth functions, we must trade off the simplicity of a model that significantly abstracts Earth systems by modeling them with a small number of easily understood parameters with the complexity of models that attempt to include more detail of Earth functioning but contain a larger number of parameters with more technical meanings and interconnections. Choices about this tradeoff will be different depending on our purpose. Climate modelers who use models to test their detailed understanding of Earth functioning will obviously choose to work with more complicated models. Decision makers who have have to include many factors beyond the climate in there work, may be better served by simpler models that capture the well understood behavior of the climate.